Non mi stancherò mai di ripetere che il conto economico per l’installazione di una macchina va fatto considerando tutti i parametri, quindi è opportuno considerare soprattutto il costo energetico annuale per farla funzionare.
A maggior ragione quando si sceglie una pompa fanghi o pompa di trasferimento che normalmente funziona molte ore al giorno.
Questo perché attratti dal costo iniziale della macchina ci dimentichiamo di considerare – per un bilancio corretto – quanto mi costa farla funzionare.
E’ la stessa cosa che fronteggiamo quando dobbiamo fare il calcolo di quale auto ci conviene acquistare, dobbiamo considerare sia il costo iniziale dell’automobile, ma dobbiamo anche sapere quanto consuma ed in base al nostro chilometraggio annuale faremo un calcolo di convenienza.
Se questo lo facciamo a livello personale, a maggior ragione a livello industriale è doveroso farlo per non incorrere in spiacevoli sorprese che si scoprono durante l’utilizzo.
E’ quindi bene fare un piccolo schema riepilogativo per capire quale sia la soluzione migliore nella scelta di una pompa fanghi.
Facciamo un esempio numerico:
| OPZIONE A | OPZIONE B |
| Pompa Centrifuga | Pompa a Pistoni |
| 35 mc/h 6 bar 17 kW Costo: 6000 € | 30 mc/h 6 bar 8.6 kW Costo: 26000 € |
Per prima cosa dobbiamo sapere quanto è il costo (lordo) di 1 kWh di potenza.
Questo dipende da quale è la nostra fascia di appartenenza, ma possiamo usare dei valori medi desumibili visitando ad esempio il sito di Arera in cui si trova la relazione annuale Arera / elaborazione con dati Eurostat.
Scopriamo il costo lordo (con le imposte) di 1 kWh.
Supponiamo che sia ad esempio 0.19 €/kWh
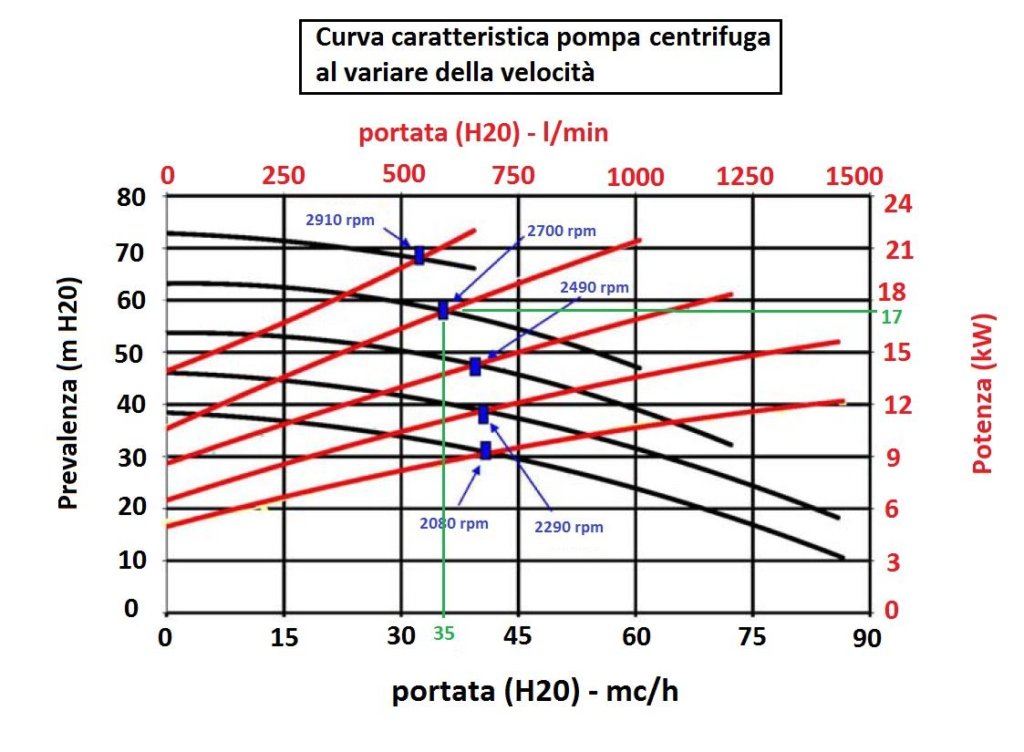
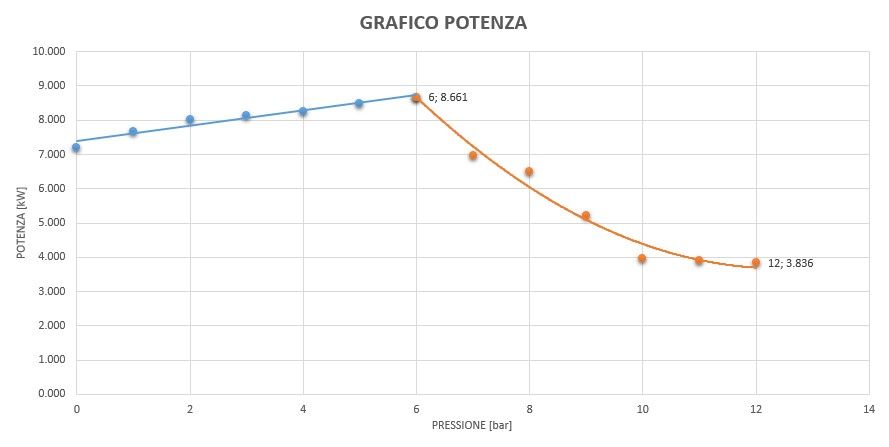
A questo punto devo sapere quante ore al giorno funziona il mio impianto e parimenti quanti giorni/anno in modo da ottenere le ore annuali di funzionamento
Esempio:
Funzionamento impianto: 8h/day – 320 day/year
da cui 8*320 = 2560 h/year di funzionamento impianto
Consumo pompa A:
17 kW * 2560 h = 43520 kWh
Consumo pompa B:
8.6 kW * 2560 h = 22016 kWh
Costo energetico pompa A:
43520 kWh * 0.19 €/kWh = 8268.80 €
Costo energetico pompa B:
22016 kWh * 0.19 €/kWh = 4183.04 €
Già da questo vediamo come la pompa B, sebbene costi di più, ha un costo annuale energetico che è la metà della pompa A. Quindi in definitiva, ogni anno con la pompa B hai in tasca € 4085.76 in più rispetto alla pompa A.
La domanda è quindi: quando è che la scelta della pompa B diventa più economica in assoluto rispetto alla pompa A? Semplice, basta fare una proiezione dei costi annuali su di un orizzonte temporale di ad esempio 10 anni
PROSPETTO COSTI INCREMENTALE
| ANNO | POMPA A (€) | POMPA B (€) |
| 0 | 6000 | 26000 |
| 1 | 14268.80 | 30183.04 |
| 2 | 22537.60 | 34366.08 |
| 3 | 30806.40 | 38549.12 |
| 4 | 39075.20 | 42732.16 |
| 5 | 47344.00 | 46915.20 |
| 6 | 55612.80 | 51098.24 |
| 7 | 63881.60 | 55281.28 |
| 8 | 72150.40 | 59464.32 |
| 9 | 80419.20 | 63647.36 |
| 10 | 88688.00 | 67830.40 |
A questo specchietto è meglio associare un semplice grafico che mostra molto più chiaramente cosa avviene:
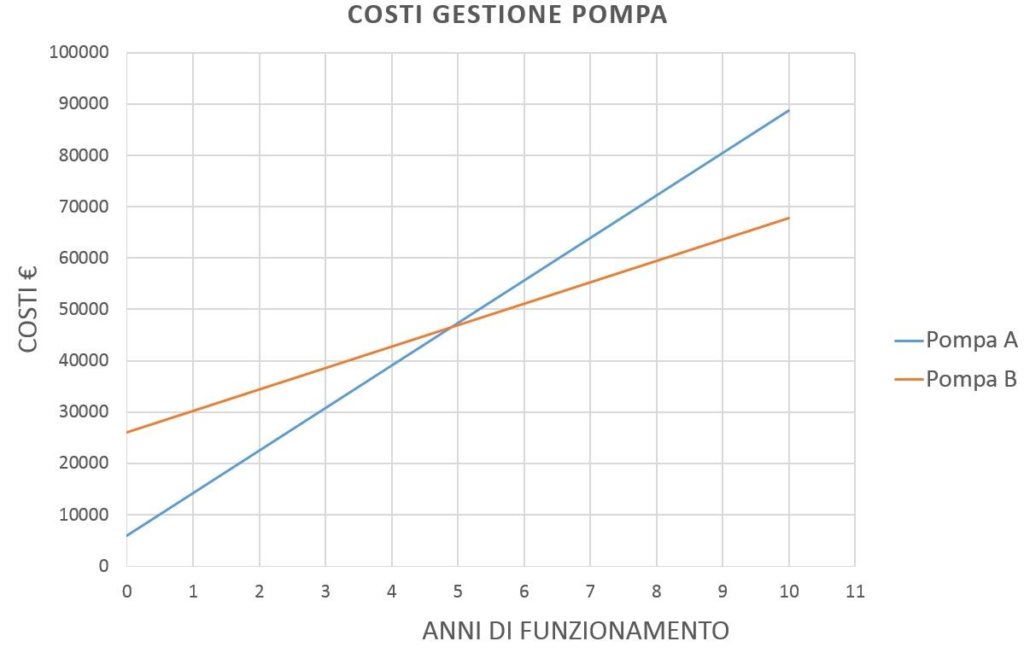
Come visibile, al 5° anno i costi delle due soluzioni si equivalgono. Questo significa che a partire dal 5° anno, se utilizzo la Pompa B, ogni anno risparmio € 4085.76 di costi energetici.
Visto che la vita utile di una buona pompa a pistoni se trattata bene può arrivare anche a 20 anni significa che alla fine dei 20 anni ho risparmiato rispetto alla soluzione A ben 15*4058.76 = 60881,4 €.
Questo è fatto considerando 8h di funzionamento al giorno e con i costi energetici appena visti. Chiaramente più utilizzo la pompa e più la forbice si allarga.
La funzione che rappresenta il costo economico di una pompa durante il suo funzionamento (a parte il costo della manutenzione) è in prima approssimazione una semplice retta la cui pendenza è il costo annuale della pompa stessa:
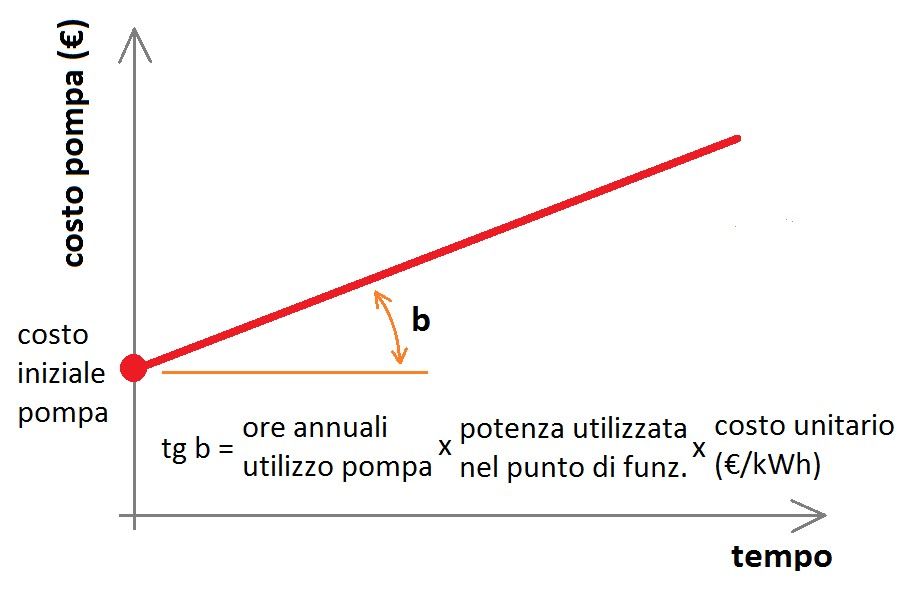
Per calcolare analiticamente il punto di pareggio basta uguagliare le due rette che rappresentano rispettivamente la pompa A e la pompa B.
costo A = c.iniz.A + tg b1 * t
costo B = c.iniz.B + tg b2 * t
ricavando t avrò che:
t = (c.iniz.B – c.iniz.A)/[ore annuali utilizzo pompa*(pot.A – pot.B)*costo unitario €/kWh]
quindi numericamente, con i valori dell’esempio precedente:
t = (26000-6000) € / [2560 h/year * (17 kW – 8.6 kW)* 0.19 €/kWh] = 4.89 year
Ecco che analiticamente abbiamo trovato il lasso temporale a partire dal quale la pompa B inizia ad essere vantaggiosa economicamente rispetto alla pompa A (4.89 anni nel nostro caso)
Ti è piaciuto questo articolo?
Vorresti scaricare GRATUITAMENTE il nostro e-book sulle filtropresse a piastre e sulle pompe di alimentazione dove è compreso l’intero articolo oltre a molti altri contenuti? Clicca qui e vai alla pagina del download!