No me cansaré de repetir que la declaración de la renta para la instalación de una máquina debe hacerse considerando todos los parámetros, por lo que es recomendable considerar sobre todo el gasto energético anual para hacerla funcionar.
Más aún al elegir una bomba de lodos o una bomba de transferencia que normalmente funciona muchas horas al día.
Esto se debe a que, atraídos por el costo inicial de la máquina, nos olvidamos de considerar, para un presupuesto correcto, cuánto cuesta hacerla funcionar.
Es lo mismo a lo que nos enfrentamos cuando tenemos que calcular qué coche nos conviene más comprar, tenemos que considerar tanto el coste inicial del coche, pero también tenemos que saber cuánto consume y en función de nuestro kilometraje anual hará un cálculo de conveniencia.
Si esto lo hacemos a nivel personal, más aún a nivel industrial es necesario hacerlo para no toparse con sorpresas desagradables que se descubren durante el uso.
Por lo tanto, es bueno hacer un pequeño diagrama de resumen para comprender cuál es la mejor solución para elegir una bomba de lodos.
Hagamos un ejemplo numerico:
| OPCIÓN A | OPCIÓNB |
| Bomba centrífuga | Bomba de pistón |
| 35 mc/h 6 bar 17 kW Costo: 6000 € | 30 mc/h 6 bar 8.6 kW Costo: 26000 € |
Primero necesitamos saber cuánto es el costo (bruto) de 1 kWh de energía.
Esto depende de a qué banda pertenezcamos, pero podemos utilizar valores medios que se pueden inferir visitando, por ejemplo, la web de Arera donde se encuentra el informe anual de Arera/tratamiento con datos de Eurostat.
Averigüemos el costo bruto (con impuestos) de 1 kWh.
Supongamos que es por ejemplo 0,19 €/kWh
En este punto necesito saber cuantas horas al dia trabaja mi sistema y tambien cuantos dias/año para poder obtener las horas anuales de operacion
Ejemplo:
Operación de la planta: 8h/día – 320 día/año
de los cuales 8*320 = 2560 h/año de operación de la planta
Consumo bomba A:
17kW * 2560h = 43520kWh
Consumo bomba B:
8,6kW * 2560h = 22016kWh
Bomba de costo de energía A:
43520 kWh * 0,19 €/kWh = 8268,80 €
Bomba de costo de energía B:
22016 kWh * 0,19 €/kWh = 4183,04 €
De esto ya vemos como la bomba B, aunque cuesta más, tiene un gasto energético anual que es la mitad de la bomba A. Así que al final, cada año con la bomba B tienes 4085,76 € más en el bolsillo que con la bomba A.
Por lo tanto, la pregunta es: ¿cuándo la elección de la bomba B se vuelve absolutamente más barata que la bomba A? Simple, basta con hacer una proyección de los costes anuales en un horizonte temporal de, por ejemplo, 10 años
Declaración de costes adicionales
| AÑO | BOMBA (€) | BOMBA (€) |
| 0 | 6000 | 26000 |
| 1 | 14268.80 | 30183.04 |
| 2 | 22537.60 | 34366.08 |
| 3 | 30806.40 | 38549.12 |
| 4 | 39075.20 | 42732.16 |
| 5 | 47344.00 | 46915.20 |
| 6 | 55612.80 | 51098.24 |
| 7 | 63881.60 | 55281.28 |
| 8 | 72150.40 | 59464.32 |
| 9 | 80419.20 | 63647.36 |
| 10 | 88688.00 | 67830.40 |
Es mejor asociar este espejo con un gráfico simple que muestra mucho más claramente lo que sucede:
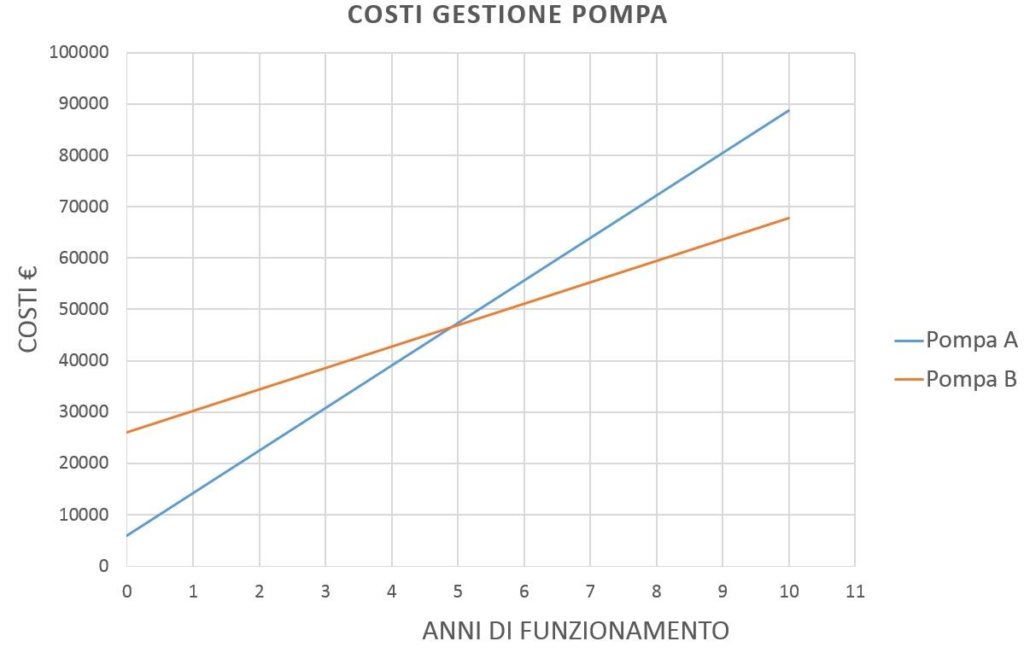
Como puede verse, en el 5º año los costes de las dos soluciones son iguales. Esto significa que a partir del 5º año, si uso la Bomba B, ahorro 4085,76 € en costes de energía cada año.
Dado que la vida útil de una buena bomba de pistón, bien tratada, puede llegar incluso a los 20 años, esto significa que al cabo de los 20 años he ahorrado 15*4058,76 = 60881,4€ respecto a la solución A.
Esto se hace considerando 8h de operación por día y con los costos de energía recién vistos. Claramente, cuanto más uso la bomba, más se amplía la brecha.
La función que representa el coste económico de una bomba durante su funcionamiento (aparte del coste de mantenimiento) es en primera aproximación una recta simple cuya pendiente es el coste anual de la propia bomba:
Para calcular analíticamente el punto de equilibrio, es suficiente igualar las dos líneas que representan la bomba A y la bomba B respectivamente.
coste A = inicial c.A + tg b1 * t
costo B = c.init.B + tg b2 * t
derivando t tendré que:
t = (c.iniz.B – c.iniz.A)/[horas anuales de uso bomba*(pot.A – pot.B)*coste unitario €/kWh]
luego numéricamente, con los valores del ejemplo anterior:
t = (26000-6000) € / [2560 h/año * (17 kW – 8,6 kW)* 0,19 €/kWh] = 4,89 año
Aquí hemos encontrado analíticamente el marco temporal a partir del cual la bomba B empieza a ser económicamente ventajosa frente a la bomba A (4,89 años en nuestro caso)